White-Box Cryptography

Recent advances shared at CHES 2021 on white box cryptography
In usual scenarios, keys and cryptographic algorithms are executed in special environments, properly isolated from the outside world. Indeed, rich environments are not reliable and can be controlled by attackers. This is the case of applications executed by a smartphone, which may contain malware, backdoors, etc. and are therefore likely to be manipulated by an attacker to read the secret keys or modify the public keys. Typical secure elements are Trusted Platform Modules (TPMs), Hardware Security Modules (HSMs), or even Secure Elements (SEs). The current trend is to even bury the SEs in rich applicative chips, so that they are out of reach of peripheral attacks.
The SEs therefore become integrated Secure Elements (iSEs).
In some contexts, typically software implementations, cryptographic algorithms must operate in untrusted environments, without any support from an integrated secure element. This occurs when security is not end-to-end, for example due to certain legacy designs. In such cases, in order to perform computations securely, operational constraints require that the secret key be embedded into the cryptographic algorithm. This requirement is very strong: the WBC implementation shall resist key extraction even if the source code of the algorithm entangled with the key is completely disclosed.
Primer on White-Box Cryptography
Such implementations are called White-Box Cryptography (WBC). One technique to devise WBC consists in the algorithm’s tabulation specialized for its key, followed by obfuscation of the resulting tables. The obfuscation results from the application of invertible diffusion and confusion layers at the interface between tables so that the input/output analysis does not provide exploitable information about the concealed key material. The first white-box cryptography implementations were performed by Chow, Eisen, Johnson, and van Oorschot. They were applied on DES and AES block ciphers.
Initially, the principle of white-box cryptography was to protect software implementations, which are very amenable to code disclosure (attack called code lifting). However, white-box cryptography has also been repurposed to protect embedded firmware or even hardware implementations. Still, the idea is that the attacker will either manage to read intermediate values in the implementation or correlate them directly or through side-channel analysis.
Several protections of this type have been proposed in the past and already cryptanalyzed thanks to a complete analysis of the WBC scheme. It is possible to classify attacks on WBC into three categories:
- Statistical attacks (similar to cryptanalysis techniques);
- Those based on techniques from grey-box analysis (i.e., side-channel or fault injection analyses), such as differential fault analysis (DFA), differential computation analysis (DCA), collision or mutual information, or high-order computational attacks;
- Those which rely on Fourier transforms.
We have chosen to develop the third category of attacks, in that we show that they are very well suited to attacking a WBC scheme based on tables dissimulation.
Operation to hide
Let’s focus on a simple protection pattern, namely the white-boxing of the AES T-box (composition of the byte-level S-box with a linear μ diffusion operating from 1 to 4 bytes). The operation we therefore consider for being white-boxed is thus this algorithmic step:
x → T(x⊕k*) = μ ◦ S(x⊕k*), where x and k* are the correct keys.
It is easy to extract the correct k* from the table of 256 words of 32-bit. Indeed, there are only 256 tables, each corresponding to a key.
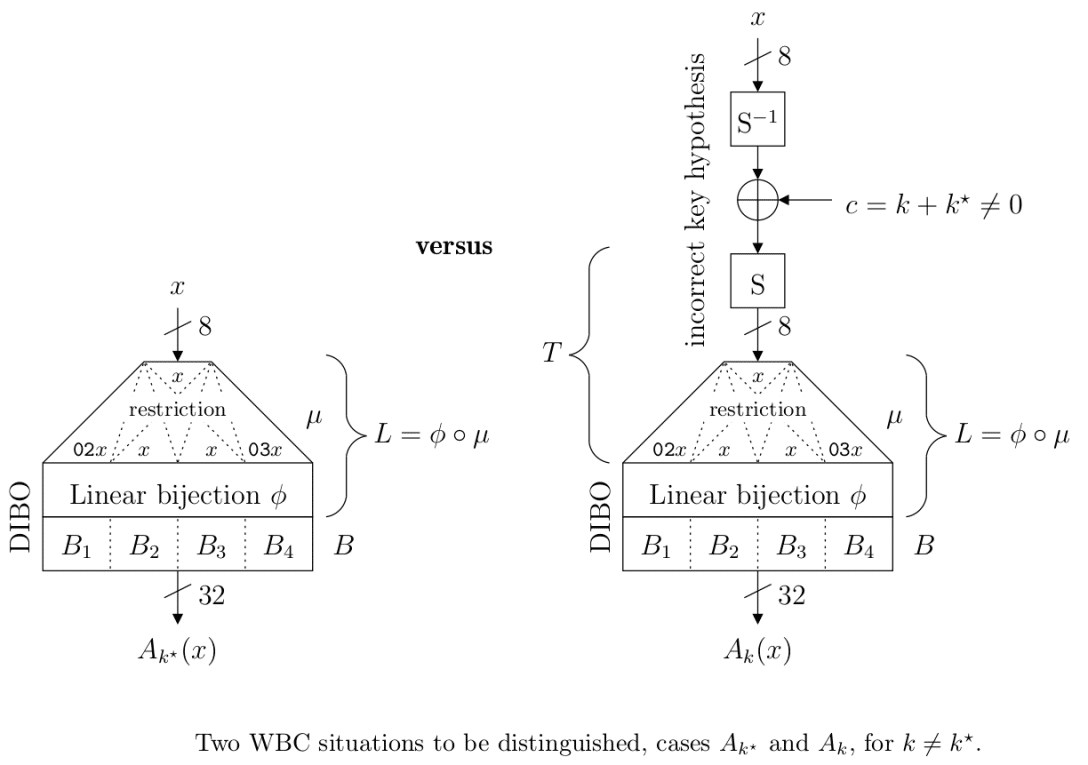
In the Diffused Input Blocked Output (DIBO) white-boxing concept, the secret k* is concealed by applying an internal encoding, which consists in applying a random secret permutation ϕ to the output of the T-box and then of a second secret function B designed by blocks of small random permutations applied in parallel to the 32-bit words.
The attacker tries to peel off the T function, and is left to determine which key is singular among the 256 Ak tables defined as: x→ B ◦ L ◦ S (S−1 ((y) ⊕ (k ⊕ k*)), where L is the linear function obtained by chaining μ and ϕ.
Attack
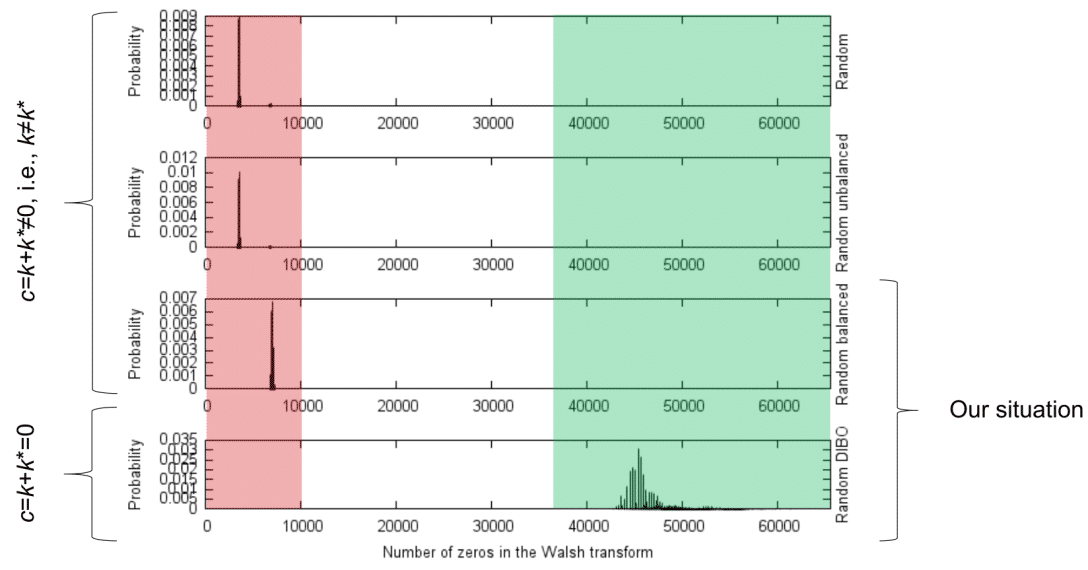
It turns out that the spectrum of the tables Ak is rich in zeros when the key is guessed correctly (k = k*), and when one of the sub functions Li is NOT invertible. This might seem paradoxical, since the whole function is invertible. However, the restrictions might not be.
This leads to a spectral distinguisher, as represented in the figure below.
Now, how often is Li not invertible? It happens that it is very likely, precisely in 99.3% of the time. Indeed, the attack succeeds if any of the four component 8 → 8 is not balanced.
Mitigation
The mitigation is therefore very simple. It consists in making sure that the four bijections Li (i ∈ {1,2,3,4}) are all invertible. This represents 0.7% of the cases, but it still represents a wealth of configurations of L and B, namely 262 of them. Thus, the DIBO protection is still effective to conceal k* in the table.
To sum up, we have introduced a new distinguisher for AES T-box obfuscated by a random DIBO function. It consists in counting the null values in a Walsh-Hadamard spectrum of a guess function.
We have justified why such an enumeration makes sense in the context of WBC. Then, we have proved that it works as long as at least one restriction (out of four) of the DIBO linear part to external blocked bijections is not invertible. In this respect, we have concluded the mathematical research to explain the reason for the success of spectral attacks in the field of DIBO; first and foremost, our characterization of weak vs strong linear parts solves the remaining open problem stated in the research of Lee, Jho and Kim in IEEE Access 2020.
In such situation (which happens >99% of the time), we have shown mathematically that our attack always works. On the opposite, we have indicated that when the four linear restrictions are all bijective, then our attack (and others, such as correlation attacks) fails. This can happen even without jeopardizing the entropy in the linear (diffusion) part of DIBO. Hence, this is a new recommendation to make sure that WBC schemes based on DIBO obfuscation are safe. Thus, we have repaired the DIBO obfuscation scheme against spectral attacks.
The effectiveness of our attack is supported by a thorough analysis of the distinctive feature of DIBO (when at least one Li does not have full rank) compared to a random function.
Complete article on white box cryptography by Sylvain Guilley is available online
Do you have questions on this topic and on our protection solutions? We are here to help.